Konfidenzintervalle einfach erklärt
Inhaltsverzeichnis
zurück zur Übersicht
Unsere Spezialisten unterstützen dich dabei, eine herausragende wissenschaftliche Arbeit abzuliefern.

Easy Thesis unterstützt dich beim Schreiben deiner Abschlussarbeit. Du wirst es lieben!
Einleitung
Konfidenzintervalle oder auch Vertrauensintervalle gehören zur Inferenzstatistik. Wenn auf Basis der Stichprobe die Parameter für die Grundgesamtheit geschätzt werden, geben Konfidenzintervalle einen Bereich an, in dem der wirkliche Erwartungswert, die Varianz oder andere Werte mit einer gewissen Wahrscheinlichkeit liegen.
In diesem Artikel wird erklärt, was Konfidenzintervalle sind, was sie aussagen und wie man sie bestimmt.
Bringe deine Noten auf das nächste Level!
Lass deine Arbeit von Lektorat Plus verbessern und sichere dir den Schlüssel zu akademischem Erfolg. 🎓
Mehr erfahren
Definition Konfidenzintervalle
Häufig ist es in der Statistik nicht möglich, die komplette Grundgesamtheit zu befragen. Daher bedient man sich einer Stichprobe, aus der man Parameter wie Erwartungswert, Varianz, Median oder andere Werte errechnet. Auf Basis dieser Stichprobenwerte können mit Hilfe eines Schätzverfahrens diese Werte auch für die Grundgesamtheit veranschlagt werden. Da es sich hierbei um Punktschätzungen handelt, wird der wahre Wert nahezu nie gleich der Schätzung sein, aber in der Nähe davon liegen.
Mit Hilfe eines sogenannten Konfidenzintervalls definiert man einen Bereich oder ein Intervall, bei dem man davon ausgehen kann, dass der wahre Wert mit einer hohen Wahrscheinlichkeit darin liegt.
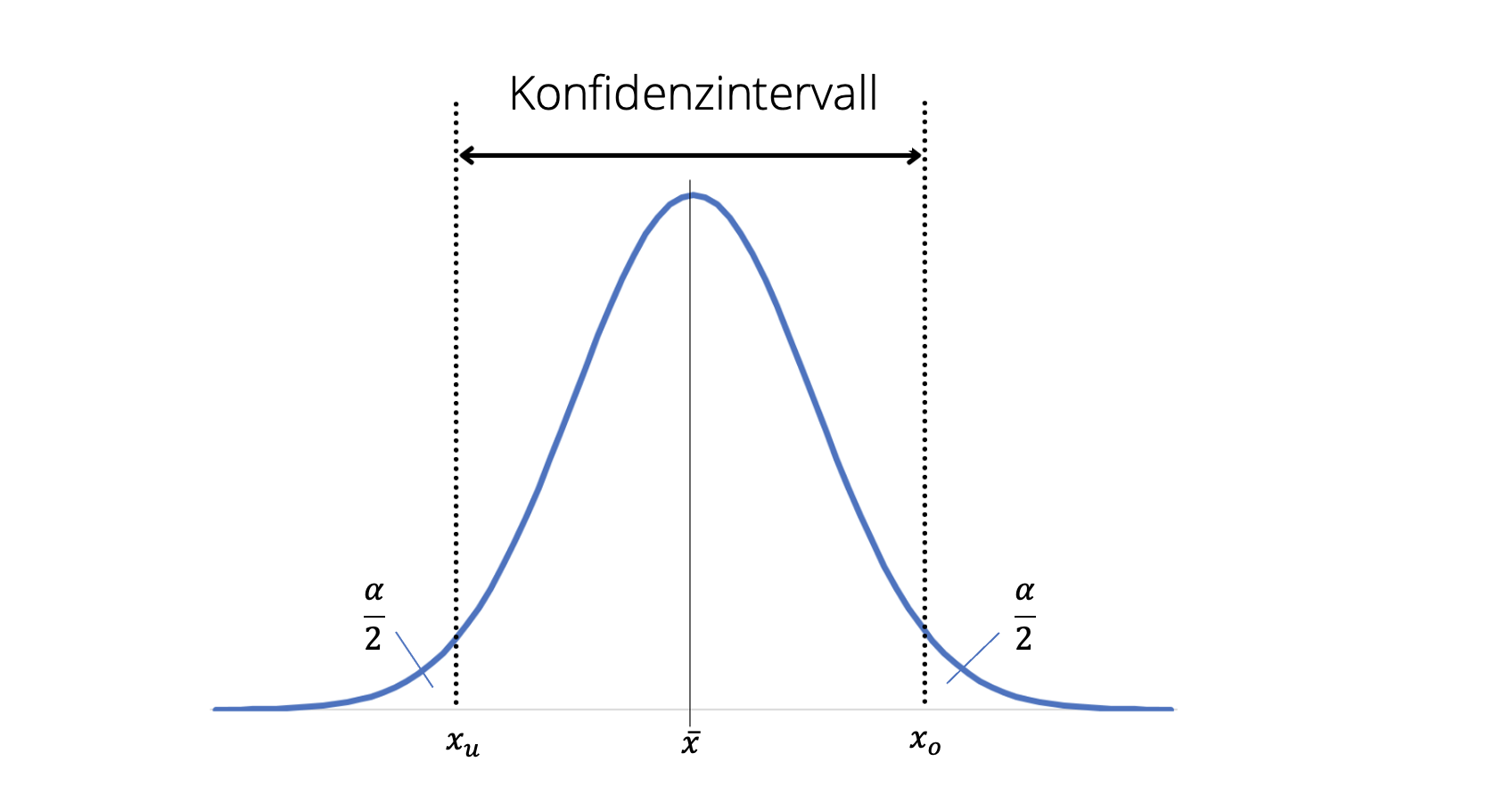
Die Wahrscheinlichkeit, mit der ein Mittelwert darin liegt, heißt Konfidenzniveau, als Dezimalzahl Konfidenzkoeffizient. Die Wahrscheinlichkeit, mit der ein Parameter nicht darin liegt, wird als Irrtumswahrscheinlichkeit α angegeben.
Konfidenzintervalle werden auch Vertrauensintervalle oder Vertrauensbereiche genannt. Das dazugehörige Konfidenzniveau wird genauso als Vertrauenswahrscheinlichkeit bezeichnet. Häufig findet man für das Konfidenzintervall auch die Abkürzung KI.
Es handelt sich beim Vertrauensintervall um ein statistisch berechnetes Intervall, das hilft einzuschätzen, wo der wahre Mittelwert liegt. Dies ist nötig, da Hypothesen und Prognosen, die auf Basis der Stichprobe berechnet wurden, für die Grundgesamtheit ebenfalls valide gelten sollen. Würde man verschiedene Stichproben aus einer Grundgesamtheit ziehen, werden deren Mittelwerte immer minimal unterschiedlich sein, aber in demselben Vertrauensintervall liegen. Man kann also sagen, dass das Vertrauensintervall die Schwankungsbreite des Mittelwertes angibt.
Vereinfacht wird oft davon gesprochen, dass der wahre Wert mit einer gewissen Wahrscheinlichkeit, z.B. 95%, in diesem Konfidenzintervall liegt. Korrekterweise wäre ein Konfidenzintervall mit 95%iger Wahrscheinlichkeit ein Intervall, das den wahren Parameter mit einer Wahrscheinlichkeit von 95% enthält, wenn man es sehr häufig mit neuen Stichproben berechnet. Ein einzelnes Intervall wäre also nur mit 95%iger Wahrscheinlichkeit ein Intervall, das den wahren Parameter enthält.
Konfidenzintervalle können sowohl für den Mittelwert als auch für den Median und die Varianz berechnet werden. Da Vertrauensintervalle am häufigsten für den Mittelwert eingesetzt werden, gehen wir im Folgenden nur darauf ein.
Arten von Konfidenzintervallen
Bevor man ein Konfidenzintervall berechnet, muss festgelegt werden, mit welcher Wahrscheinlichkeit der wahre Wert in diesem Intervall liegen soll. In der Statistik werden hierfür meistens Wahrscheinlichkeiten von 95% oder 99% hergenommen.
Soll der wahre Wert mit einer Wahrscheinlichkeit von 95% in dem Vertrauensintervall liegen, spricht man von einem 95% Konfidenzintervall, bei einer Wahrscheinlichkeit von 99% von einem 99% Konfidenzintervall
Berechnung von Konfidenzintervallen
Allgemein werden Konfidenzintervalle ermittelt, indem man einen Bereich um den errechneten Stichprobenparameter definiert. Das Konfidenzintervall ist meist symmetrisch zu diesem Punkt und je nach Varianz der Stichprobe und des gewünschten Konfidenzniveaus enger oder breiter.
Das Konfidenzintervall hat immer eine obere und eine untere Grenze, die es vom Bereich der Irrtumswahrscheinlichkeit trennen. Diese Grenzen sind ebenfalls Zufallsvariablen und werden nach folgender Formel berechnet:
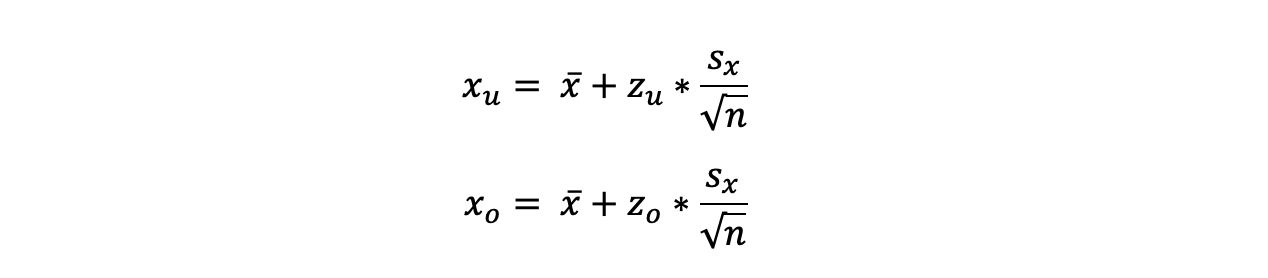

Während n feststeht und x ̅ sowie s_x aus der Stichprobe berechnet werden, werden die transformierten Intervallgrenzen z_u/ z_o in der Tabelle der Standardnormalverteilung unter dem entsprechenden Konfidenzniveau nachgeschlagen (siehe Beispiel).
Durch den zentralen Grenzwertsatz (siehe Artikel zur Normalverteilung), kann man ab einer ausreichend großen Stichprobe immer mit der Normalverteilung rechnen. Ist die Stichprobe zu klein (n < 50), wird anstatt der Normalverteilung mit der t-Verteilung (siehe Artikel zur t-Verteilung) gerechnet und statt der z-Werte werden die t-Werte entsprechend nachgeschlagen.
Beispiel
Berechnen wir das Konfidenzintervall anhand eines fiktiven Beispiels. Wir interessieren uns für die monatlichen Mietausgaben von Studierenden in Deutschland. Da es uns nicht möglich ist, sämtliche Studierende zu befragen, schätzen wir diesen Wert auf Basis einer Stichprobe. Dafür befragen wir deutschlandweit zufällig 100 Studierende. Wir berechnen auf Basis der Daten 341€ als mittlere monatliche Mietausgabe (x ̅, siehe Artikel zu den Lageparametern). Daraus ermitteln wir eine Standardabweichung von 16,1€ (s_x, siehe Artikel zu den Streuparametern).
Auf Basis dieser Werte wollen wir die wahren monatlichen Mietausgaben schätzen. Wir definieren ein Vertrauensintervall von 95%, also wollen einen Bereich finden, der – vereinfacht gesagt – mit einer Sicherheit von 95% den tatsächlichen Wert enthält.
Mit 100 Studierenden können wir auf Basis des zentralen Grenzwertsatzes auf jeden Fall von der Normalverteilung ausgehen.
Wir nutzen die Formeln:


Die z-transformierten Werte schlagen wir in der Tabelle nach (hier ein Auszug aus der Verteilungstabelle):

Da wir 95% als Konfidenzniveau festgelegt haben, ergibt sich eine Irrtumswahrscheinlichkeit von 5% also 0,05. Der wahre Wert kann sowohl nach oben als auch nach unten abweichen und da wir ein symmetrisches Intervall abbilden wollten, teilen sich die 5% Irrtumswahrscheinlichkeit auf jeweils 2,5% nach oben und nach unten auf. Also schlagen wir bei 0,975 (97,5%) nach und erhalten einen z-Wert von 1,960 für die obere Grenze. Da die Normalverteilung symmetrisch zur x-Achse ist, können wir für die untere Grenze, den symmetrisch gespiegelten, also negativen, Wert von z = -1,960 annehmen.
Wir setzen die Werte in die Formeln ein:
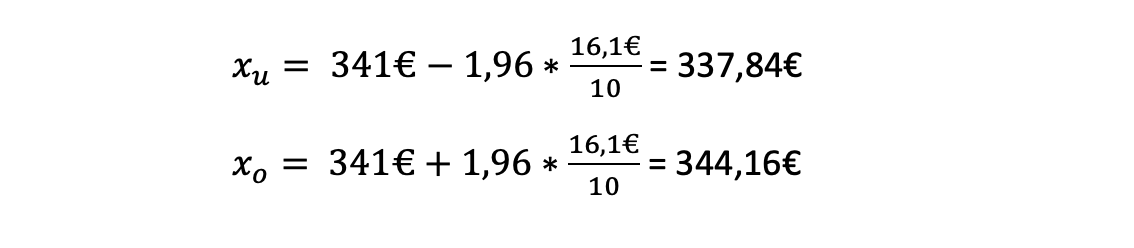
Mit einer Wahrscheinlichkeit von 95% liegen die tatsächlichen monatlichen Mietausgaben also in einem Vertrauensintervall von 337,84€ und 344,16€.

Zusammenfassung
Parameter wie Erwartungswert, Varianz oder Median einer Grundgesamtheit können meist nur auf Basis von aus der Stichprobe berechneten Werten geschätzt werden. Der wahre Wert fällt nahezu nie exakt mit der Schätzung zusammen, liegt aber in der Nähe. Mit Hilfe von Konfidenz- oder Vertrauensintervallen werden Bereiche definiert, die den wahren Wert mit einer hohen Wahrscheinlichkeit enthalten.
Zur Berechnung der Konfidenzintervalle wird im ersten Schritt das Konfidenzniveau, also die entsprechende Wahrscheinlichkeit definiert und anschließend werden die Intervallgrenzen berechnet. Häufig geschieht dies für standardnormalverteile Mittelwerte.
Gib deiner Arbeit den Feinschliff, den sie verdient.
Entfalte das volle Potenzial deiner schriftlichen Arbeiten mit Lektorat Plus und sichere dir den Weg zu einer herausragenden Note.
Jetzt Dokument hochladen