Varianz, Standardabweichung und Spannweite – die wichtigsten Streuungsmaße
Inhaltsverzeichnis
- Einleitung
- Einleitung
- Varianz
- Standardabweichung
- Varianzkoeffizient
- Spannweite
- Quartilsabstand
- Beispiel
- Zusammenfassung

Unsere Spezialisten unterstützen dich dabei, eine herausragende wissenschaftliche Arbeit abzuliefern.

Easy Thesis unterstützt dich beim Schreiben deiner Abschlussarbeit. Du wirst es lieben!
Einleitung
Der Begriff der Streuungsmaße ist in der deskriptiven Statistik zu finden und fasst eine Vielzahl von Begriffen zusammen. Streuungsmaße geben die Ausbreitung und
Streuung der Beobachtungswerte an. Die wichtigsten Vertreter sind die Varianz, die Standardabweichung und die Spannweite.
Weiterhin werden in diesem Artikel auch die Begriffe Quartilsabstand und Varianzkoeffizient erklärt, erläutert wie man sie berechnet und interpretiert.
Bringe deine Noten auf das nächste Level!
Lass deine Arbeit von Lektorat Plus verbessern und sichere dir den Schlüssel zu akademischem Erfolg. 🎓
Mehr erfahren
Begriffsdefinition
- Streuungsmaße werden auch als Streuparameter oder Dispersionsmaße bezeichnet.
Während die Lageparameter angeben, wo in der Verteilung Mittelwert oder Zentralwert liegen, geben Streuungsmaße Aufschluss darüber, welche Abweichungen die Werte voneinander haben bzw. wie nah oder entfernt sie voneinander sind. Dies ist für viele Analysen relevant, um die Verteilung, die Streuung, aber auch die Qualität der Messung anzugeben. Die Streuung kann einerseits um einen Lageparameter, wie bei Standardabweichung und Varianz um den Mittelwert, oder über die gesamte Breite der Verteilung angegeben werden.
Bevor die einzelnen Begriffe und ihre Berechnung näher erläutert werden, muss man eine wichtige Unterscheidung zwischen Parameter der Stichprobe und Parameter der Grundgesamtheit bzw. der Verteilung treffen.
Bei der Analyse einer Stichprobe und bei der Analyse einer Grundgesamtheit werden unterschiedliche Begriffe beziehungsweise Vorgehensweisen verwendet. Bei einer Stichprobe kennt man nur die tatsächlichen Ausprägungen anhand einer begrenzten Anzahl von Werten. Die eigentlichen Parameter wie Verteilung, Erwartungswert und Varianz können nur geschätzt werden. Entsprechend treten auch Unsicherheiten auf, die über die Formel korrigiert werden, wie später beschrieben.
Sprechen wir von der Stichprobe, so berechnen wir die empirische Varianz bzw. die Stichprobenvarianz. Die einzelnen Parameter werden wie folgt benannt:

Analysieren wir die Grundgesamtheit, ist häufig der Mittelwert bekannt, teilweise sind es auch Verteilung und Streuungsmaße.
In der Regel wird auch nicht mehr mit dem Anteil der Beobachtungswerts an der Stichprobe (1/(n-1) oder 1/n) gerechnet, sondern mit der
relativen Häufigkeit pi, die somit eine Gewichtung der einzelnen Ausprägungen vornimmt.
Die einzelnen Parameter werden nun anders bezeichnet:

Varianz
Die Varianz wird als mittlere quadratische Abweichung oder gewichtete quadratische Abweichung vom Mittelwert definiert. Sie liefert eine grobe Abschätzung, wie weit die einzelnen Werte des Zufallsexperiments vom Erwartungswert entfernt liegen.
Da sie in der quadratischen Dimension bzw. Einheit des Beobachtungswertes liegt, ist sie in der Praxis meist wenig aussagekräftig, dafür wird die Standardabweichung hergenommen. Wir betrachten zuerst die Varianz einer kleinen Stichprobe.
Die Formel hierfür lautet:
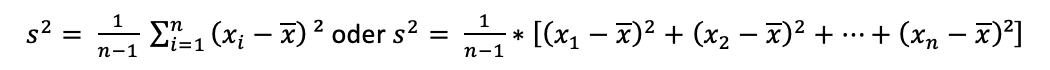

Bei kleinen Stichproben erfolgt somit eine Schätzung der Varianz. Meist handelt es sich hierbei jedoch um eine Unterschätzung, weshalb man n-1 als Korrekturfaktor statt n hernimmt. Bei großen Stichproben ist die Schätzung der Varianz genauer, weshalb man den Korrekturfaktor nicht mehr benötigt und stattdessen rechnet:
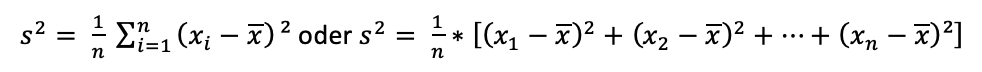
Wie bereits erläutert wurde, rechnet man bei der Grundgesamtheit mit anderen Parametern, es ändert sich

Die Formel verändert sich zu:
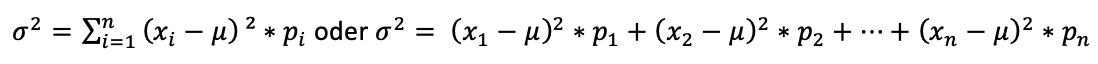
Standardabweichung
Die Standardabweichung s ist die Wurzel aus der Varianz s².Sie beschreibt die durchschnittliche Abweichung von Mittelwert und hat die gleiche Dimension/Einheit wie die Beobachtungswerte.
Je kleiner die Standardabweichung, desto näher liegen die Werte beisammen. Eine Standardabweichung von 0 ist jedoch sehr unwahrscheinlich, da in der Regel immer Messfehler oder Abweichungen vorhanden sind.
Die Formel dafür lautet:
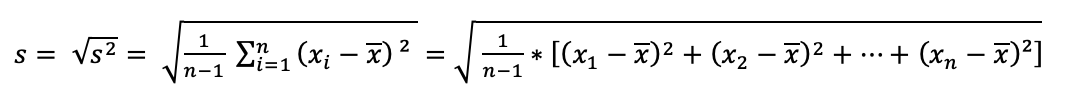
Für große Stichproben ergibt sich entsprechend:
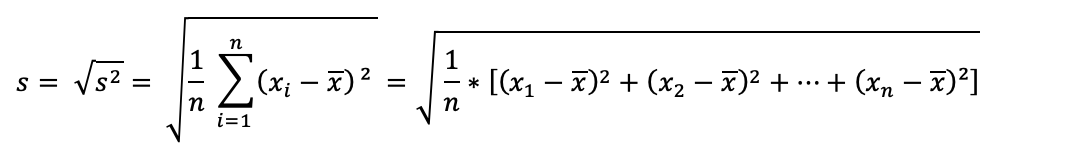
Für Berechnungen oder Analysen der Grundgesamtheit:
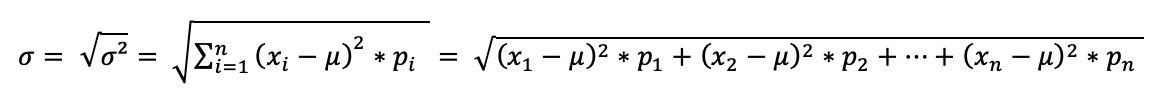
Varianzkoeffizient
Ähnlich wie die Standardabweichung gibt der Varianzkoeffizient die Streuung der Daten um den Mittelwert an. Im Gegensatz zur Standardabweichung ist er jedoch ohne Einheit und kann somit eine relative Auskunft über die Streuung geben.
Er berechnet sich, indem man die Standardabweichung durch den Mittelwert teilt, also:

Der Varianzkoeffizient gibt somit das Verhältnis von Standardabweichung zum Mittelwert an. Je kleiner er ist, desto näher liegen die Werte beisammen, je größer, desto weiter auseinander. Ein Wert von 1 oder größer würde beispielsweise bedeuten, dass die Standardabweichung größer als der Mittelwert ist.
Spannweite
Zusätzlich zu Varianz und Standardabweichung gibt es auch zwei Werte, die die absolute Ausdehnung der Werte angeben: Spannweite und Quartilsabstand.
Die Spannweite gibt Aufschluss darüber, wie weit die Werte maximal auseinander liegen, also wie viel zwischen dem größten und kleinsten Wert liegt.
Dementsprechend wird sie aus der Differenz zwischen dem größten und dem kleinsten Wert gebildet. Die Spannweite kann sowohl mit SP (=Spannweite) als auch mit R (=Range) angegeben werden.
Die Formel für die Berechnung lautet:
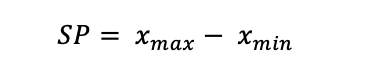
Die Spannweite gibt lediglich an, in welchem Bereich sie die Werte befinden, aber nicht wo die meisten Werte mit welcher Wahrscheinlichkeit liegen. Außerdem kann sie durch besonders große oder besonders kleine Werte, sogenannte Ausreißer, leicht verfälscht werden. Hierfür wird häufig der Quartilsabstand hergenommen.
Quartilsabstand
Der Quartilsabstand gibt ähnlich wie die Spannweite an, in welchem Bereich die Werte liegen, lässt aber das kleinste und das größte Viertel (Quartil) weg und berechnet die Differenz dazwischen.
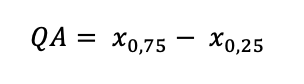
Im nun folgenden Beispiel wird dies unter anderem mit betrachtet.
Berechnung und Interpretation anhand eines Beispiels
Es werden zehn Personen nach ihrem Gewicht gefragt. Zehn Werte stellen eine relativ kleine Stichprobe dar, somit rechnen wir mit s, s² und Korrekturfaktor. Obwohl wir die Personen nicht selbst gewogen haben, sprechen wir im Folgenden von „Messwerten“.
Es ergibt sich folgende Tabelle:

Wir haben zehn Personen gefragt, also ergibt sich eine Anzahl von Messwerten n = 10. Als Basis für Varianz und Standardabweichung errechnen wir im ersten Schritt den Mittelwert ¯x. Der Einfachheit halber lassen wir die Einheiten in der Formel weg, geben sie nur im Ergebnis an und runden auf zwei Nachkommastellen.
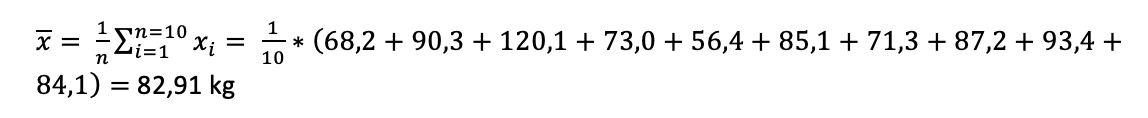
Im Durchschnitt wiegen unsere Befragten also 82,91 kg.
Berechnen wir nun Varianz und Standardabweichung:

Durchschnittlichen weicht das Gewicht der Befragten um 17,4 kg vom Erwartungswert ab. Dies ist damit zu erklären, dass wir zwei (56,4kg und 120,1kg) Werte haben, die deutlich über oder unter dem Erwartungswert liegen. Somit werden auch die Varianz und Standardabweichung größer.
Der Varianzkoeffizient ergibt sich aus:
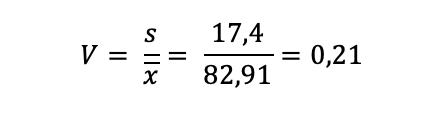
Nun berechnen wir noch die Breite der Messung:
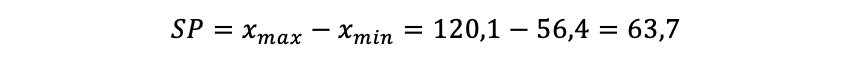
Der Unterschied zwischen der leichtesten und der schwersten Person lag also bei 63,7 kg. Da die Werte ähnlich weit vom Mittelwert entfernt sind, haben sie diesen nicht verfälscht. Aufgrund der hohen einfachen Entfernung ist jedoch die Varianz sehr hoch. Dieses Beispiel wurde bewusst gewählt, um auch den Quartilsabstand zu zeigen:
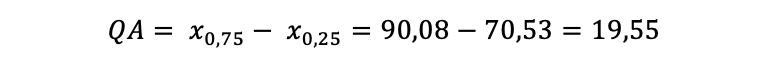
Rechnet man die extremen Ausreißer nach oben und unten mit dem 25% und dem 75% Quartil heraus, ergibt sich eine Ausbreitung von nur noch 19,55 kg zwischen dem leichtesten und schwersten Befragten.
Zusammenfassung
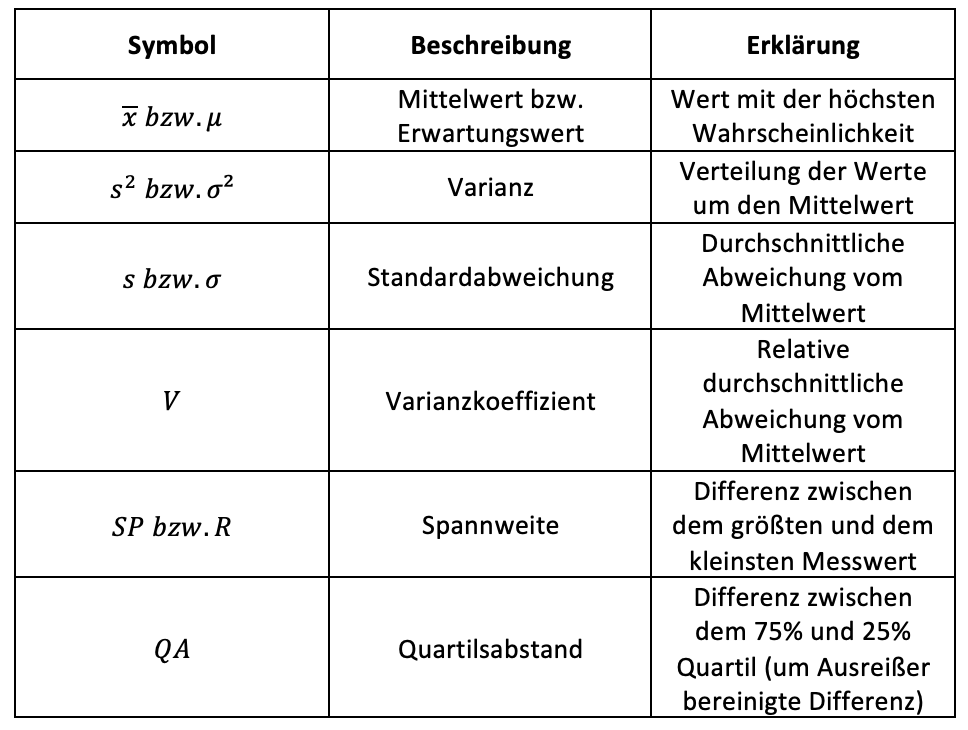
Streuungsmaße geben an, wie weit die Beobachtungswerte voneinander und auch vom Mittelwert entfernt sind. Während die Varianz eher eine grobe Abschätzung der Verteilung liefert, nennen Standardabweichung und Varianzkoeffizient exakte beziehungsweise relative Abweichungen. Die Standardabweichung in der Dimension bzw. der Einheit des Messwertes, der Varianzkoeffizient ein Verhältnis. Spannweite und Quartilsabstand beziffern die Breite der Messwerte, wobei der Quartilsabstand diese um Ausreißer bereinigt angibt.
Gib deiner Arbeit den Feinschliff, den sie verdient.
Entfalte das volle Potenzial deiner schriftlichen Arbeiten mit Lektorat Plus und sichere dir den Weg zu einer herausragenden Note.
Jetzt Dokument hochladen