Skalenniveau einfach erklärt
Inhaltsverzeichnis
- Begriff Skalenniveau
- Nominalskala
- Ordinalskala
- Intervallskala
- Verhältnisskala/ Ratioskala
- Absolutskala
- Ordnung der Skalenniveaus
- Fazit

Unsere Spezialisten unterstützen dich dabei, eine herausragende wissenschaftliche Arbeit abzuliefern.

Easy Thesis unterstützt dich beim Schreiben deiner Abschlussarbeit. Du wirst es lieben!
Misst man Variablen, so werden diese immer auf einer Skala angegeben. Je nach Variable können diese Skalen aber verschiedene sogenannte Skalenniveaus aufweisen.
In diesem Artikel wird erklärt, was Skalenniveaus sind und mit der Nominalskala, der Ordinalskala, der Intervallskala und der Verhältnisskala die wichtigsten Arten vorgestellt. Außerdem erfolgt eine Einordnung und ein Vergleich der verschiedenen Skalenniveaus.
Begriff Skalenniveau
Wird eine Variable untersucht und deren Ausprägungen gemessen, müssen diese für die Auswertung veranschaulicht werden. Dafür stellt man sie je nach der Art ihrer Ausprägung (Eigenschaft, Note, Zahl) auf einer Skala dar. In der Statistik werden verschiedene Skalenarten auf bestimmten Niveaus unterschieden. Das Skalenniveau legt fest, welche Analysen für die Auswertung der Daten möglich sind.
Je höher ein Skalenniveau, desto höher ist der Informationsgehalt und desto aussagekräftiger die Daten. Gleichzeitig ist nicht für jede Variable jedes Skalenniveau möglich. Wichtig für die Auswertung, vor allem in Statistikprogrammen, ist daher die richtige Zuordnung des Skalenniveaus. Wertet man beispielsweise die Lieblingsfarben von Kindern aus, kann das Ergebnis keine Zahl sein und umgekehrt.
Nominalskala
Die Nominalskala ist das einfachste Skalenniveau und zugleich auch das mit dem geringsten Informationsgehalt.
Die Daten auf einer Nominalskala werden in einzelne Kategorien eingeteilt, diese lassen sich jedoch nicht in eine logische Reihenfolge bringen und somit auch nicht quantitativ differenzieren.
Beispiele für nominalskalierte Variablen sind das Geschlecht, das Studienfach, der Familienstand, die Konfession, die Haarfarbe, der Wohnort, die Nationalität aber auch beispielsweise bevorzugte Schokoladensorten. Die einzelnen Ausprägungen dürfen nicht in eine Ordnung zu bringen sein und müssen eine Qualität und nicht ein Ausmaß darstellen. Das bedeutet, eine Person kann zwar männlich, weiblich oder divers sein, aber nicht mehr männlich/weiblich/divers als eine andere Person.
Man kann die Nominalskala ohne Informationsverluste transformieren , indem man den Ausprägungen Zahlen zuordnet wie 1 = männlich, 2 = weiblich, 3 = divers. Diese können beliebig gewählt werden. Man muss nur darauf zu achten, dass durch die zugeordnete Zahl der Wert nicht besser oder schlechter wird. Diese Transformation ist theoretisch mit allen Skalenniveaus möglich, jedoch wird der Informationsverlust mit zunehmendem Niveau größer.
Bei der Nominalskala kann man nur Aussagen über die Häufigkeit treffen, sprich wie häufig welcher Wert ist und welches die Ausprägung(en) mit der größten Häufigkeit ist. Rechnerische Auswertungen sind nicht möglich.
Ordinalskala
Das nächsthöhere Skalenniveau nach der Nominalskala ist die Ordinalskala.
Die Ordinalskala, oder auch Rangskala , besteht aus einzelnen Kategorien, die in eine logische Reihenfolge gebracht werden können. Eine Aussage über den Abstand zwischen den Werten ist jedoch nicht möglich.
Die Ordinalskala wird beispielsweise für Schulnoten, Plätze in einem Wettkampf oder Hochschulrankings genutzt. Man kann die Ausprägungen nach der Reihe ordnen und weiß beispielsweise, dass der Sieger eines Wettbewerbs besser war als der Zweitplatzierte. Nehmen wir an, der Silbermedalliengewinner ist eine Millisekunde später ins Ziel gekommen als der Gewinner und zehn Millisekunden vor dem dritten Platz.
Die Abstände zwischen den Teilnehmern sind also nicht gleich groß, man kann aber klar sagen, wer besser war. Man kann die Ordinalskala auch für das Messen der Produktzufriedenheit nutzen. Hierfür wird die sogenannte Likert-Skala verwendet:
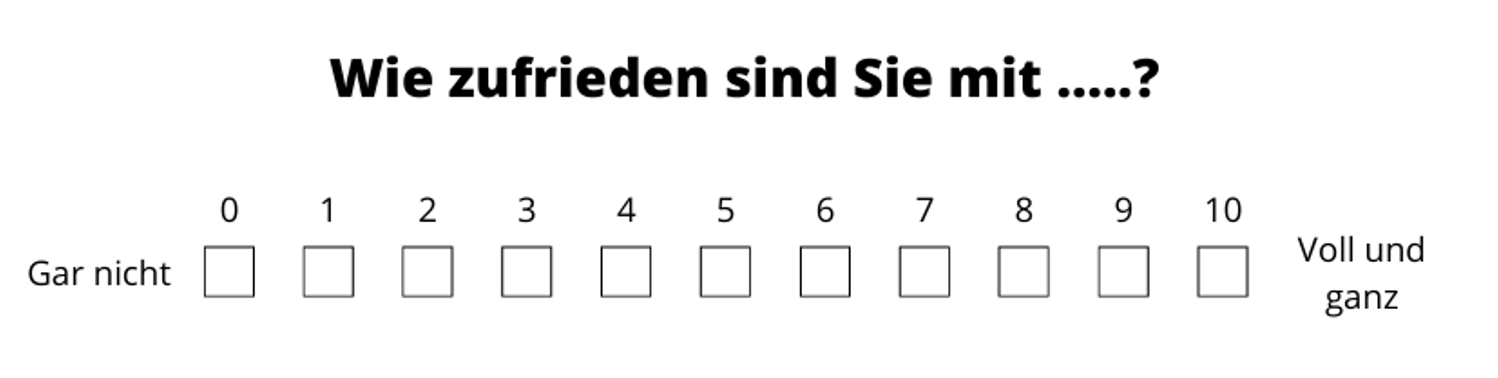
Mit ordinalskalierten Variablen kann man ebenfalls keine Rechenoperationen durchführen, aber durch die Rangreihenfolge können Häufigkeitsverteilungen und Lagemaße wie der Modus, Median, Quartile, Boxplot oder Rangkorrelationskoeffizient nach Spearman ermittelt werden.
Intervallskala
Noch genauer als die Ordinalskala ist die Intervallskala.
Eine Intervallskala kann neben den Kategorien und der Reihenfolge auch eine Aussage zu den Abständen zwischen den einzelnen Ausprägungen treffen, nicht aber zu ihren Verhältnissen.
Ein beliebtes Beispiel für die Intervallskala ist die Temperatur in Grad Celsius. Ein Grad ist immer genau gleich. Der Abstand zwischen 10 Grad zu 20 Grad ist genauso groß wie zwischen 20 Grad und 30 Grad. Da die Intervallskala nur einen willkürlichen bzw. künstlich gewählten Nullpunkt hat, können wir jedoch keine Verhältnisse abbilden. 20 Grad sind nicht automatisch doppelt so warm wie 10 Grad.
Bei der Intervallskala können wir zusätzlich das arithmetische Mittel und grundlegende Streumaße wie Standardabweichung, Varianz, Quantile oder die Spannweite berechnen.
Verhältnisskala/ Ratioskala
Das höchste gebräuchliche Skalenniveau ist die Verhältnis-,Proportional- oder Ratioskala .
Die Verhältnisskala hat alle Eigenschaften wie die Intervallskala (Kategorien, Reihenfolge, Abstände) und kann zusätzlich noch Aussagen über das Verhältnis zwischen den Ausprägungen treffen.
Im Gegensatz zur Intervallskala hat die Verhältnisskala einen absoluten und natürlich gegebenen Nullpunkt. Beispiele für die Verhältnisskala sind Alter, Einkommen, Größe, Länge oder andere biologische bzw. finanzielle Größen. Beim Einkommen wäre der natürliche Nullpunkt bei 0€ und jemand der 3.000€ verdient, erhält doppelt so viel wie jemand, der 1.500€ verdient. Auch die Temperatur kann auf einer Verhältnisskala gemessen werden, wenn man sie in Kelvin angibt.
Zusätzlich zu den schon genannten Rechenoperationen können wir auch das geometrische Mittel berechnen und multiplikative Transformationen durchführen.
Absolutskala
Die Absolutskala als Spezialfall der Verhältnisskala ist das Skalenniveau mit dem höchstmöglichen Informationsgehalt. Sie erfüllt alle Eigenschaften (stetig, quantitativ, kategorisierbar, mögliche Reihenfolge, gleicher Abstand, natürlicher Nullpunkt) und liegt meist in einer natürlichen Einheit vor. Man erkennt eine Absolutskala daran, dass sie eine bestimmte „Stückzahl“ misst, beispielsweise die Anzahl an absolvierten Fachsemstern, pro Tag gerauchten Zigaretten oder gegessenen Pizzastücken. Im Falle der Zigaretten wäre „nicht geraucht“ der absolute Nullpunkt.
Da diese Skalenart in der Praxis meist mit einer aufwendigen Vollerhebung zusammenhängen würde (sonst ist die Aussagekraft zu gering) und auch nur ein Spezialfall der Verhältnisskala ist, gehen wir an dieser Stelle nicht näher darauf ein.
Ordnung der Skalenniveaus
Die Nominalskala ist das niedrigste Skalenniveau, gefolgt von der Ordinalskala, der Intervallskala bis hin zur Verhältnisskala. Je höher das Skalenniveau, desto umfangreicher und präziser die Aussagen, die man über die dazugehörige Variable treffen kann. Ein höheres Skalenniveau schließt auch immer die Eigenschaften der niedrigeren mit ein und somit kann eine Variable eines höheren Niveaus als eine eines niedrigeren Niveaus behandelt werden. Umgedreht darf man die Rechenoperationen nur auf das jeweils höhere Niveau anwenden.
Für einen Überblick über die verschiedenen Skalenniveaus, ihre Merkmale und ihre Aussagekraft haben wir alle Punkte in einer Tabelle veranschaulicht:
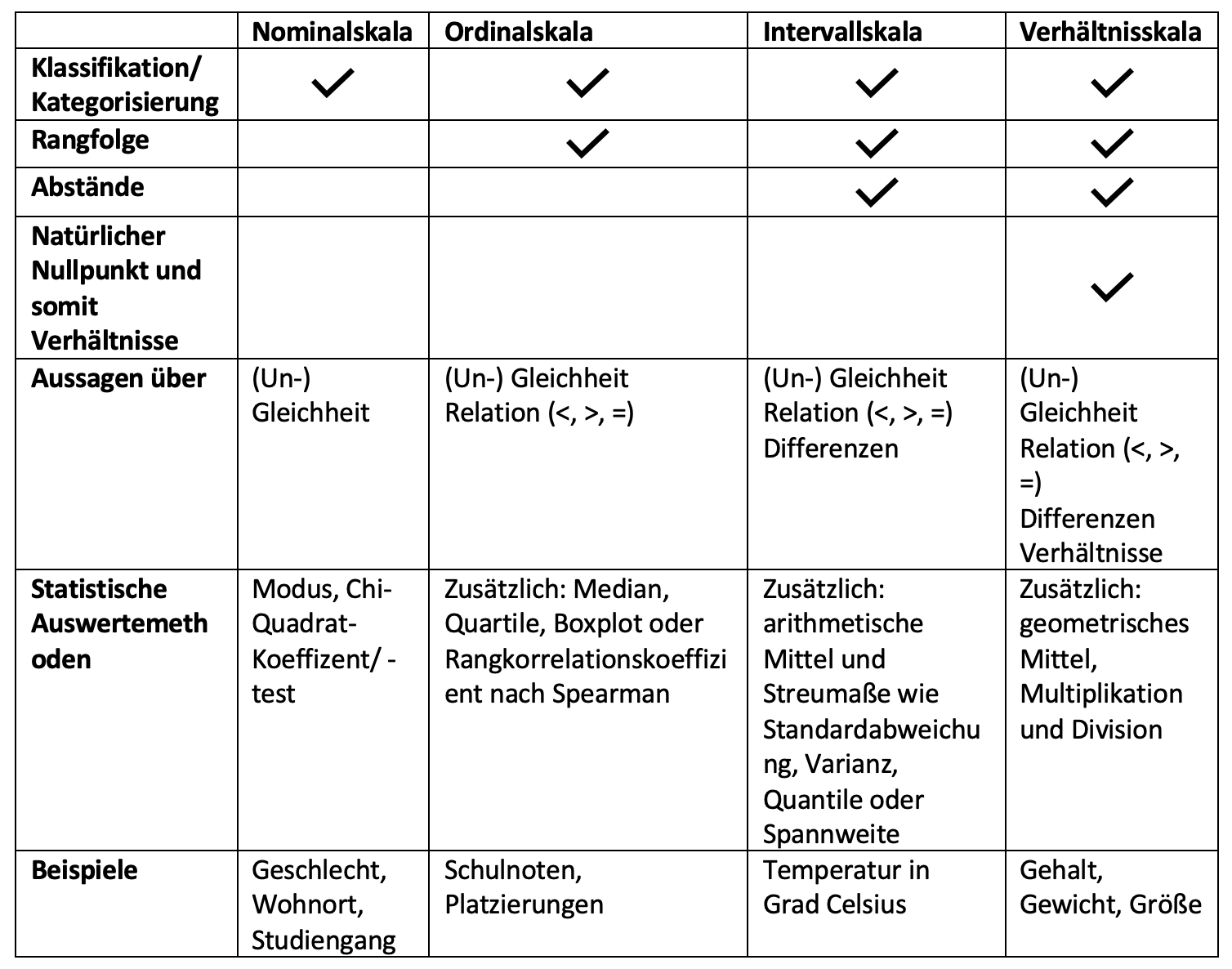
Einteilung der Skalenniveaus
Skalenniveaus lassen sich auf verschiedene Arten einteilen.
- Quantitativ vs. qualitativ
- Diskret vs. stetig
- Kategorial vs. metrisch
Diskret bedeutet, dass es keine Zwischenstufen zwischen den einzelnen Werten gibt. Stetige Variablen haben im Umkehrschluss theoretisch unendlich viele Zwischenstufen . Diskrete Variablen werden häufig auch als kategoriale Variablen bezeichnet und stetige als metrische. Die gleiche Einordnung gilt für die dazugehörigen Skalen.
- Qualitative, diskrete und somit kategoriale Skalen sind die Nominal- und die Ordinalskala.
- Quantitative, stetige und somit metrische Skalen bzw. Kardinalskalen sind die Intervall- und die Verhältnisskala.
Fazit
In der Statistik werden die Nominal-, die Ordinal-, die Intervall- und die Verhältnisskala in aufsteigender Reihenfolge unterschieden. Mit der Höhe des Skalenniveaus steigt auch der Informationsgehalt und die damit möglichen Rechen- und Auswerteoperationen.
Je höher das Skalenniveau, desto komplexer wird auch die Erhebung und die Auswertung. Für optimale Ergebnisse sollte man immer das für die Variable höchstmögliche Skalenniveau nutzen.
Gib deiner Arbeit den Feinschliff, den sie verdient.
Entfalte das volle Potenzial deiner schriftlichen Arbeiten mit Lektorat Plus und sichere dir den Weg zu einer herausragenden Note.
Jetzt Dokument hochladen