Regressionsanalyse einfach erklärt
Inhaltsverzeichnis
- Einleitung
- Anwendung
- Begriffserklärungen
- Lineare und multiple Regression
- Durchführung
- Voraussetzungen
- Zusammenfassung

Unsere Spezialisten unterstützen dich dabei, eine herausragende wissenschaftliche Arbeit abzuliefern.

Easy Thesis unterstützt dich beim Schreiben deiner Abschlussarbeit. Du wirst es lieben!
Einleitung
Die Regressionsanalyse ist ein statistisches Verfahren, das zu den multivarianten Analysemethoden gehört. Sie wird verwendet, um Zusammenhänge zwischen unabhängigen und abhängigen Variablen zu prüfen.
In diesem Artikel wird schwerpunktmäßig auf die lineare Regression und multiple Regression, weitere Arten, die Durchführung sowie die Interpretation der Ergebnisse eingegangen.
Bringe deine Noten auf das nächste Level!
Lass deine Arbeit von Lektorat Plus verbessern und sichere dir den Schlüssel zu akademischem Erfolg. 🎓
Mehr erfahren
Anwendung der Regressionsanalyse
Die Regressionsanalyse untersucht Zusammenhänge zwischen unabhängigen und abhängigen Variablen. Dabei wird meistens davon ausgegangen, dass eine oder mehrere abhängige Variablen durch einen kausalen Zusammenhang von unabhängigen Variablen bestimmt sind.
Während eine Korrelation lediglich Zusammenhänge ermittelt, kann eine Regressionsanalyse gerichtete Effekte errechnen. Sie wird hauptsächlich dazu verwendet, um einen quantitativen Zusammenhang, und dessen Stärke, zwischen Variablen zu ermitteln. Außerdem können Veränderungen der abhängigen Variablen vorausgesagt werden, wenn sich die unabhängige Variable ändert. Eine dritte Anwendung ist die Vorhersage von zukünftigen Werten.
Begriffserklärungen
Bevor wir näher auf die lineare Regression eingehen, müssen einige Begriffe und Parameter erklärt werden.
Die unabhängige Variable (UV) wird im Rahmen der Regressionsanalyse auch als Prädiktor, Ursache oder Regressor bezeichnet, während die abhängige Variable (AV) auch Zielvariable, Wirkung oder Regressand genannt wird.
Häufig liest man den Begriff der Residuen. Dieser bezeichnet die Abweichung(en) eines (mathematischen) Modells oder empirischen Werten vom tatsächlich beobachten Wert.
Für die Beschreibung der Regressionsfunktion sind die Parameter α und β als Regressionskoeffizienten relevant.
α, manchmal auch als β0, Interzept oder Konstante bezeichnet, ist der y-Achsenabschnitt (Schnittpunkt mit der Y-Achse).
Es handelt sich hierbei um den Basiswert, der eintreten würde, wenn die unabhängige Variable gleich 0 ist.
Die Steigung ß ist der Regressionskoeffizient der UV, also die durchschnittliche Zunahme der abhängigen Variablen, wenn die unabhängige Variable um eine Einheit erhöht wird.
Weiterhin sind die Begriffe des Korrelationskoeffizienten r und des Bestimmtheitsmaßes (Determinationskoeffizient) r² für die Regressionsanalyse relevant. Sie geben Aufschluss über die Güte des Regressionsmodells.
Der Korrelationskoeffizient r (siehe Artikel zur Korrelation)
ist ein Maß für Größe und Richtung des Zusammenhangs
Das Bestimmtheitsmaß r² ist eine wesentliche Maßzahl für die Qualität des Regressionsmodells. Es sagt aus, wie viel Prozent der AV durch die UV beschrieben werden können.
Genauer gesagt ermittelt es, welcher Anteil der Gesamtvarianz durch die Varianz des Modells erklärt wird.
Entsprechend berechnet sich r² aus diesem Verhältnis:
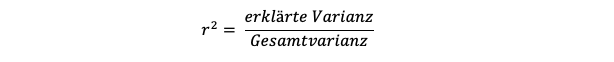
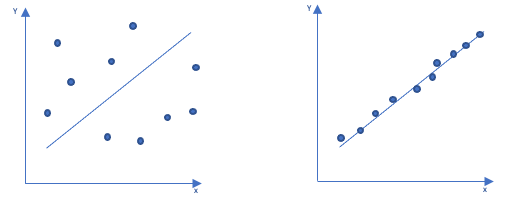
Die linke Grafik zeigt ein Beispiel für eine geringe erklärte Varianz, die rechte ein Beispiel für eine hohe erklärte Varianz.
Liegen mehrere UVs vor, müssen Korrekturen aufgrund von Überschneidungen (adjustiertes Bestimmtheitsmaß) vorgenommen werden.
Arten der Regressionsanalyse
Die Regressionsanalyse hat viele verschiedene Ausprägungen, die mitunter sehr komplex werden können. Welche Analyse angewendet wird, hängt vor allem von der Anzahl der zu testenden Variablen und deren Skalenniveau ab. Zudem unterscheidet man zwischen einem linearen und nichtlinearen Zusammenhang. Lineare Regressionen folgen einer Geraden, der sogenannten Regressionsgeraden. Die nichtlinearen Modelle sind mathematisch komplexer und verwenden häufig iterative Algorithmen, um immer eine möglichst einfache mathematische Funktion zu finden, die den Zusammenhang zwischen UV und AV erklärt.
Aufgrund der Komplexität wird in diesem Artikel nur auf die lineare Regression (einfach und multiple Regression) eingegangen. Einfach lineare Regression und multiple Regressionen bedingen jeweils eine metrische Skalierung der AV. Sonderformen der Regressionsanalyse sind die logistische Regressionsanalyse (diskrete Skalierung), die multivariante Regressionsanalyse (mehrere AVs) und deren Spezialfälle Moderatorenanalyse und die Mediatorenanalyse (Untersuchung, ob eine dritte Variable den Zusammenhang zwischen AV und UV beeinflusst).
Lineare Regression
- Die einfachste Form der Regressionsanalyse ist die einfache lineare Regression. Hierbei geht man davon aus, dass es genau eine UV und eine AV in Form eines linearen Zusammenhangs gibt.
Die Formel für die Regressionsgerade mit u als Fehlerterm lautet:
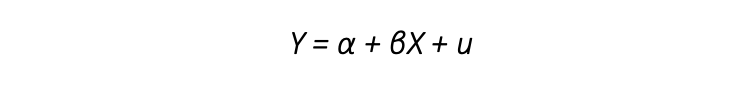
Eine lineare Regression würde beispielsweise durchgeführt werden, wenn man das Einkommen (AV) einer bestimmten Personengruppe untersuchen möchte und davon ausgeht, dass dieses lediglich vom Alter der Personen (UV) abhängt.
Multiple Regression
- Erweitert man die einfache lineare Regression um weitere UVs bei einer AV, bei einem ebenfalls linearen Zusammenhang, spricht man von einer multiplen oder auch mehrfachen Regression.
Ein wichtiges Kriterium ist, dass man bei einer multiplen Regression davon ausgeht, dass es eine lineare Unabhängigkeit zwischen den UVs gibt. Eine Korrelation der UVs kann bei der multiplen Regression unter Umständen zu hohen Standardfehlern der Regressionskoeffizienten führen und die Einflüsse einer der UV auf die AV sind nicht mehr eindeutig zu erkennen.
Die multiple Regression wird mit folgender Formel beschrieben:
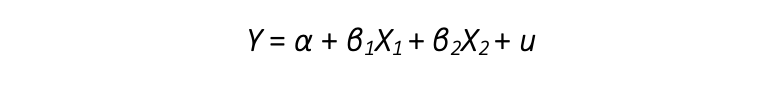
Die Formel ist sehr ähnlich zur einfachen linearen Regression. Es werden lediglich weitere Variablen mit den Termen βnXn angehängt. Eine multiple Regression findet häufiger Anwendung, da in der Regel mehrere UVs einen Zusammenhang erklären.
Nehmen wir das Beispiel aus der linearen Regression mit dem Einkommen als AV und dem Alter als UV und erweitern es um weitere UVs, wie beispielsweise der Berufserfahrung in Jahren, würden wir von einer multiplen Regression sprechen.
Durchführung
Die lineare Regression kann händisch oder durch digitale Programme wie SPSS, Excel, R Studio oder ähnliche durchgeführt werden.
Eine lineare Regression besteht aus mehreren Teilen. Im ersten Schritt wird das Regressionsmodell festgelegt, im zweiten Schritt werden die Parameter für die Regressionsanalyse ermittelt und im dritten Schritt werden die Ergebnisse überprüft.

Zu Beginn wird festgelegt, was die zu untersuchende abhängige Variable ist (bzw. mehrere Variablen sind) und welche Faktoren in Form einer unabhängigen Variablen Einfluss darauf haben könnten. Ebenso wird die Art der Regressionsanalyse gewählt, also ob beispielsweise eine einfache lineare, eine multiple Regression oder ein komplexeres Modell Anwendung findet.
Im zweiten Schritt werden die geschätzten Parameter des Modells ermittelt. Dies kann entweder grafisch bzw. händisch über eine geschätzte Funktion oder rechnerisch über Programme ermittelt werden. Händisch würde man versuchen eine Funktion zu zeichnen und die Parameter abzulesen. Ein Datenanalysetool würde beispielsweise über die Methode der kleinsten Quadrate eine Funktion bestimmten und die Parameter errechnen.
Im dritten Schritt überprüft man die in der linearen Regression ermittelten Werte sowie das Modell. Dafür berechnet man r² und führt einen F- und einen t-Test durch.
Erhält man ein r² nahe 0, würde dies bedeuten, dass die UVs nicht richtig ausgewählt wurden. Im Gegenzug ist ein Wert von 1 ebenfalls selten, da typischerweise mehrere komplexe Einflussfaktoren vorliegen und ein Zusammenhang nicht von einigen wenigen Faktoren komplett erklärt wird.
Weiterhin wird im Rahmen der Regressionsanalyse geprüft, ob die erklärte Varianz durch einen Zusammenhang zwischen den Variablen zustande gekommen oder rein zufällig ist. Man überprüft mit Hilfe des F-Tests (siehe Artikel zur ANOVA) die Signifikanz, also die Aussagekraft von r² und ob es systematisch verschieden zu 0 ist. Ist der Wert der Signifikanz unter 0,05 ist das Modell kein Zufall und hängt genau von diesen Koeffizienten ab.
Der letzte Bestandteil der Prüfung der Ergebnisse ist die Signifikanz bzw. Aussagekraft der Parameter. Die Fragestellung ist, ob sich die Parameter signifikant von 0 unterscheiden. Ist dies beispielsweise beim Steigungsparameter β nicht der Fall, würde dies bedeuten, dass die UV keinen Effekt auf die AV hat. Hierzu wendet man einen t-Test (siehe Artikel zum t-Test). Es werden nicht die Mittelwerte miteinander verglichen, sondern die Regressionsparameter. α und β werden separat voneinander getestet, indem man jeweils den empirischen Koeffizienten mit 0 (kein Effekt) vergleicht. Bei der multiplen Regression werden entsprechend auch die weiteren Parameter getestet. Als sehr vereinfachte Faustregel kann festgehalten werden, dass ein t von >+2 oder <-2 für eine signifikante Abweichung von 0 spricht.
Voraussetzungen
Damit eine lineare Regression oder eine multiple Regression tragfähige Ergebnisse liefert, müssen einige Voraussetzungen erfüllt sein:
- Skalenniveau: AV und UV sind mindestens intervallskaliert
- Ausreichend Daten aus einer zufälligen Stichprobe: mehr Beobachtungswerte als zu ermittelnde Parameter. Außerdem sind alle möglichen UVs im Modell einbezogen
- Erwartungswert der Residuen (Fehler) ist 0
- Homoskedastizität also Homogenität der Varianz der Residuen
- Keine Korrelation unter den Residuen
- Normalverteilung der Variablen: als Voraussetzung für t- und F-Tests
Zusammenfassung
Eine Regressionsanalyse ermittelt den Zusammenhang zwischen UVs und AVs. Sie wird zur Beschreibung des Zusammenhangs oder zur Berechnung weiterer Werte herangezogen.
Abhängig von der Anzahl der jeweiligen Variablen und des Skalenniveaus gibt es verschiedene Verfahren. Die wichtigsten sind die einfache lineare und die multiple Regression.
Um diese durchzuführen, wird ein Modell beschrieben, die Funktion und ihre Parameter berechnet und anschließend über Bestimmtheitsmaß, F-Test und t-Test auf ihre Signifikanz
und Aussagefähigkeit geprüft. Lineare und multiple Regression liefern nur tragfähige Ergebnisse, wenn einige Voraussetzungen bezüglich Variablen und Residuen erfüllt sind.
Gib deiner Arbeit den Feinschliff, den sie verdient.
Entfalte das volle Potenzial deiner schriftlichen Arbeiten mit Lektorat Plus und sichere dir den Weg zu einer herausragenden Note.
Jetzt Dokument hochladen