Korrelation und Kausalität
Inhaltsverzeichnis
zurück zur Übersicht
Unsere Spezialisten unterstützen dich dabei, eine herausragende wissenschaftliche Arbeit abzuliefern.

Easy Thesis unterstützt dich beim Schreiben deiner Abschlussarbeit. Du wirst es lieben!
Einleitung
Korrelation und Kausalität sind zwei zentrale Grundbegriffe aus der Statistik. Beide sind wichtig, um Zusammenhänge zwischen Variablen in Datensätzen zu beschreiben.
Da beide Begriffe inzwischen auch den Weg in unsere Alltagssprache gefunden haben, besteht häufig die Gefahr, dass wir sie etwas unsauber benutzen oder gar verwechseln. Dieser Artikel erklärt den Unterschied zwischen den beiden Begriffen und macht deutlich, warum es wichtig ist, dass wir sie nicht durcheinander bringen.
Bringe deine Noten auf das nächste Level!
Lass deine Arbeit von Lektorat Plus verbessern und sichere dir den Schlüssel zu akademischem Erfolg. 🎓
Mehr erfahren
Korrelation
- Von Korrelation spricht man, wenn ein Zusammenhang zwischen zwei Variablen erkennbar ist.
Die Variablen können prinzipiell für alles stehen, was sich irgendwie messen lässt. Körpergröße oder Alter können Variablen sein, aber ebenso auch die Einstellung gegenüber einer politischen Partei oder der Waldbestand auf einer bestimmten Fläche.
Es gibt sowohl positive Korrelation als auch negative Korrelation. Bei der positiven Korrelation steigen die Werte der abhängigen Variable Y mit steigenden Werten der unabhängigen Variable X.

Bei der negativen Korrelation verhält es sich genau umgekehrt, die Werte der unabhängigen Variable Y sinken mit steigenden X-Werten.
Ein statistischer Zusammenhang (im Sinne einer Korrelation) sagt allerdings an sich noch nichts darüber aus, ob die zwei betrachteten Variablen tatsächlich direkt miteinander in Zusammenhang stehen.
Das wird auch anhand des folgenden Beispiels deutlich.
In Gegenden, in denen viele Einfamilienhäuser stehen, gibt es viele Siebenschläfer. Die Anzahl von Einfamilienhäusern korreliert
also (positiv) mit der Anzahl der Siebenschläfer. Man könnte nun aus diesem Zusammenhang vorschnell schließen, dass er etwa dadurch begründet ist, dass Siebenschläfer besonders
gern in der Nähe von Einfamilienhäusern schlafen, da sie dieses Umfeld gemütlich finden.
Das ist aber natürlich völliger Unsinn. Die Ursache für die Korrelation liegt nämlich woanders.
Einfamilienhäuser stehen eher in ländlichen Gegenden, wohingegen Mehrfamilienhäuser eher im urbanen Raum zu finden sind. Siebenschläfer leben aber auch eher im ländlichen Raum und schon gar nicht in der Stadt.
Andere Beispiele für Korrelationen wären etwa die Anzahl von Schlafstunden und der Wochentag (am Wochenende schlafen viele Menschen deutlich länger als an Werktagen) oder der Preis einer Wohnung und ihre Größe in Quadratmetern.
Korrelationen lassen sich nahezu überall finden. Wichtig ist, dass man von einer Korrelation niemals automatisch auf Kausalität schließen darf. Denn die Welt ist sehr komplex und es gibt meistens sehr viele Faktoren, die eine bestimmte Tatsache bedingen oder beeinflussen können.
Dennoch spielt die Korrelation in der Statistik eine bedeutende Rolle, um herauszufinden und zu überprüfen, ob ein Zusammenhang besteht. Man kann auch den Grad der Korrelation auch messen. Dafür gibt es verschiedene statistische Verfahren und Kennzahlen, wie etwa den Korrelationskoeffizienten.
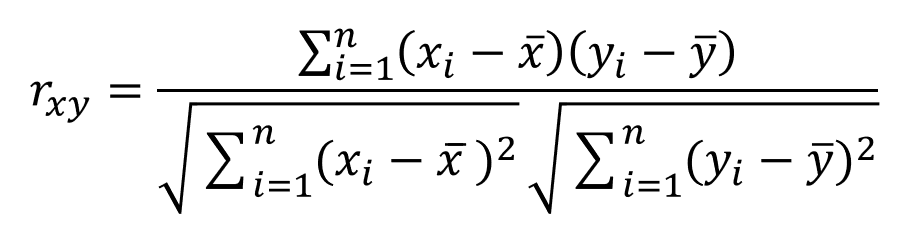
Korrelationskoeffizienten nach Pearson (siehe Wikipedia für weitere Infos)
Bei komplexen Sachverhalten kann die Stärke der Korrelation manchmal ein Indiz dafür sein, ob tatsächlich ein Sinnzusammenhang besteht.
Kausalität
- Eine Kausalität liegt dann vor, wenn eine spezielle Art von Zusammenhang herrscht. Nämlich ein Ursache-Wirkungs-Zusammenhang.
Dieser ist zwar in der Realität häufig weniger eindeutig als in der Theorie oder als in physikalischen bzw. naturwissenschaftlichen Experimenten, aber es gibt ihn. Eine Variable ist die Ursache oder die Bedingung für eine andere Variable.

Wie bereits erwähnt, kann eine starke Korrelation auf einen kausalen Zusammenhang hindeuten, muss das aber nicht. Die Aufgabe guter Forschung ist es, herauszufinden, ob es sich bei Zusammenhängen um Kausalität handelt oder nicht. Dafür untersucht man beobachtete Zusammenhänge. Es geht darum, die Wechselwirkungen, gegenseitiges Bedingen und Kausalität zu verstehen und erklären zu können.
Dafür braucht man in der Regel ein Modell, welches möglichst viele Faktoren berücksichtigt, die außer der betrachteten unabhängigen Variable auch einen Einfluss auf die abhängige Variable haben (könnten). Doch es gibt keinen allgemein gültigen Weg, um zu überprüfen, ob Kausalität vorliegt. Die Untersuchung richtet sich immer nach dem Gegenstand selbst. Die Wissenschaft hat inzwischen jedoch eine Sammlung von Werkzeugen erschaffen, die dabei helfen können, auf Kausalität zu prüfen.
Dazu zählen etwa
- statistische Methoden,
- die Randomisierung von Stichprobenziehungen und Einteilung auf Untersuchungs- bzw. Kontrollgruppe,
- sowie verschiedene Gütekriterien, die Objektivität garantieren sollen.
Zwischen der Anzahl der Stunden von körperlicher Aktivität (Sport) pro Monat und dem Körpergewicht einer Person besteht eine negative Korrelation. Jemand der tendenziell mehr Sport treibt, wiegt tendenziell weniger. Um herauszufinden,
ob diese Korrelation auf Kausalität basiert, müsste man nun folgendermaßen vorgehen.
Zunächst müssten alle erdenklichen Faktoren gesammelt werden. Beispiele hierfür sind etwa die Art der Ernährung, die Körpergröße, das Alter, der Körperbau. All diese Faktoren müssten auch in das Modell einbezogen werden,
welches für die (statistische) Untersuchung des Zusammenhangs herangezogen wird. Wenn man nun die sogennanten Drittvariablen kontrolliert und der Zusammenhang immer noch deutlich ersichtlich ist, kann man davon ausgehen, dass ein kausaler Zusammenhang vorliegt.
Eine andere Herangehensweise wäre, die Kausalität an sich zu verstehen. Dafür müsste man biologische Untersuchungen anstellen, die sich mit den Effekten von Sport auf den Körper und dessen Masse befassen. Gelangt man zu der Erkenntnis, dass durch Sport Fett verbrannt und dadurch das Körpergewicht dezimiert wird, kann man von Kausalität sprechen.
Weitere Beispiele für Kausalität sind etwa
- der Einfluss von Kohlenstoffdioxid in der Atmosphäre auf die Erderwärmung,
- der Effekt von zuckerhaltiger Ernährung auf das Risiko einer Diabeteserkrankung,
- sowie der Effekt des Bildungsabschlusses auf die Höhe des Einkommens.
Zusammenfassend lässt sich festhalten, dass jede Kausalität zwar auch eine Korrelation ist, dasselbe umgekehrt allerdings nicht gilt.
Fazit
Korrelationen treten sehr häufig auf und können sowohl auf einen (systematischen) Zusammenhang hindeuten, als auch rein zufällig bedingt sein. Seriöse Wissenschaft sollte stets genau hinsehen und mit allen ihr zur Verfügung stehenden Mitteln überprüfen, ob es sich um Kausalität, also um einen Ursache-Wirkungs-Zusammenhang handelt.
Für uns ist es elementar wichtig, die Wirkweise von kausalen Zusammenhängen zu verstehen, um unerwünschte Effekte zu unterbinden oder Missstände zu beheben. Wenn nicht klar ist, welche Dinge sich ursächlich gegenüber anderen verhalten, ist die Wahrscheinlichkeit hoch, dass Maßnahmen auf falsche oder irrelevante Zusammenhänge angewandt werden.
Allerdings können auch als sicher geglaubte kausale Zusammenhänge bei einem späteren Erkenntnisgewinn widerlegt oder zumindest aufgeweicht werden. Als Beispiel hierfür kann der von Einsteins Relativitätstheorie ausgelöste Paradigmenwechsel in der Physik betrachtet werden.
Gib deiner Arbeit den Feinschliff, den sie verdient.
Entfalte das volle Potenzial deiner schriftlichen Arbeiten mit Lektorat Plus und sichere dir den Weg zu einer herausragenden Note.
Jetzt Dokument hochladen