Boxplot verstehen und interpretieren
Inhaltsverzeichnis
- Einleitung
- Definition Boxplot
- Die Box
- Der Querstrich – der Median
- Antennen (Whisker)
- Ausreißer
- Beispiel
- Zusammenfassung

Unsere Spezialisten unterstützen dich dabei, eine herausragende wissenschaftliche Arbeit abzuliefern.

Easy Thesis unterstützt dich beim Schreiben deiner Abschlussarbeit. Du wirst es lieben!
Einleitung
Der Boxplot ist eine grafische Darstellungsform in der Statistik, die alle robusten Lage- und Streumaße in einer Abbildung veranschaulicht. In diesem Artikel wird erklärt, was ein Boxplot ist, aus welchen Elementen er besteht sowie diese jeweils zu interpretieren sind
Bringe deine Noten auf das nächste Level!
Lass deine Arbeit von Lektorat Plus verbessern und sichere dir den Schlüssel zu akademischem Erfolg. 🎓
Mehr erfahren
Definition Boxplot
Der Boxplot veranschaulicht in einem Diagramm mit dem Median und dem ersten sowie dritten Quartil alle robusten Lage- und Streumaße.
Im Boxplot wird grafisch die Datenverteilung eines mindestens ordinal skalierten Merkmals dargestellt. Der Boxplot kann schnell einen Eindruck darüber vermitteln, in welchem Bereich die untersuchten Daten liegen und wie sie sich über diesen verteilen. Veranschaulicht man mehrere Boxplots nebeneinander, eignet er sich auch zum Vergleich der jeweiligen Verteilungen.
Der Boxplot wird häufig auch als Kastengrafik, Kastendiagramm, oder nach seinen Bestandteilen, als Box-Whisker-Plot bezeichnet.
Ein Boxplot besteht aus einem Rechteck, der sogenannten Box und zwei Linien, die das Rechteck verlängern und als Antennen bezeichnet werden. Innerhalb der Box findet man den Median in Form eines Strichs und außerhalb manchmal noch Ausreißer und extreme Ausreißer. Die Darstellungsform mit dem Median, zwei Quartilen, welche die Box begrenzen, und den beiden Extremwerten wird auch als Fünf-Punkte-Zusammenfassung bezeichnet. Der Boxplot kann entweder vertikal oder horizontal dargestellt werden.
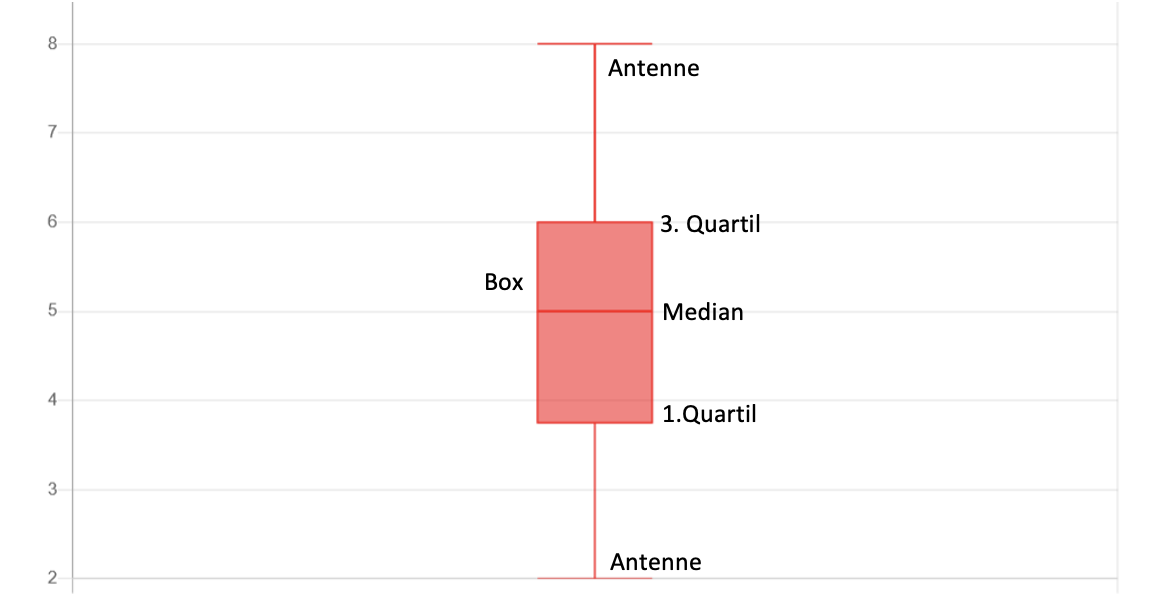
Die Box
Die Box spannt den Interquartilsabstand auf, also den Abstand zwischen dem dritten bzw. oberen Quartil und dem ersten bzw. unteren Quartil und repräsentiert somit immer die mittleren 50% der Daten
Die Länge der Box entspricht also der Differenz der beiden Quartile und ist ein Maß für die Streuung der Daten. Der Interquartilsabstand wird auch als Zwischenquartilsspanne bezeichnet und häufig als IQR abgekürzt, nach dem englischen Begriff interquartile range.
Das dritte Quartil wird auch als 75%-Quartil bezeichnet, da 75% der Werte kleiner bzw. gleich dem Quartil sind und 25% größer oder gleich. Im Umkehrschluss wird das erste Quartil als 25% Quartil bezeichnet.
Der Querstrich – der Median
Der Median wird in einem Boxplot durch einen Strich bzw. eine Linie innerhalb der Box dargestellt und teilt die gesamte Verteilung in zwei gleich große Hälften.
Der Median, oder zweites Quartil, ist der Mittelpunkt (siehe Artikel zu den Lageparametern) der Verteilung. 50% der Werte sind kleiner oder gleich dem Median, 50% größer oder gleich. Er ist besonders robust gegenüber Ausreißern und stellt somit eine realistische und ungewichtete Mitte der Werte dar. Durch seine Lage innerhalb der Box bekommt man einen Eindruck, ob und wie schief die Verteilung ist, die den Daten zugrunde liegt. Ist der Median im linken (unteren) Teil der Box, ist die Verteilung rechtsschief, liegt er im rechten (oberen) Teil, ist sie linksschief.
Antennen (Whisker)
Oben und unten wird die Box durch zwei Linien verlängert, die jeweils mit einem Strich begrenzt sind. Diese Linien werden auch als Antennen, Fühler oder Whisker bezeichnet. Sie repräsentieren die Werte außerhalb der mittleren 50% der Daten und erstrecken sich oft – aber nicht immer – über einen größeren Bereich als die Box.
Je nach Definition sind die Antennen die Minimalwerte (untere Antenne) bzw. die Maximalwerte (obere Antenne) des Datensatzes oder repräsentieren alle Werte, die innerhalb eines Bereichs des 1,5-fachen
Interquartilsabstandes (1,5xIQR) liegen. In der Definition nach John W. Tukes sind die Antennen auf maximal 1,5xIQR beschränkt. Sie enden jedoch nicht zwangsläufig erst bei 1,5xIQR, sondern bei jeweils dem Wert,
der noch innerhalb dieses Bereichs liegt.
Dies wird anhand des später beschriebenen Beispiels noch einmal deutlich. Die Antennen sind somit nicht allein durch den IQR, sondern durch die Datenwerte bestimmt.
Daher müssen sie auch nicht zwingend gleich lang sein. Gibt es keine Werte außerhalb der Grenze von 1,5xIQR, reichen die Antennen nur bis zu den Minimal- und Maximalwerten.
Ausreißer
Ausreißer sind die Werte, die außerhalb der Antennen liegen. Je nach Definition der Antennen sind diese mindestens 1,5xIQR von der Box entfernt. Was außerhalb der Box zwischen 1,5xIQR und 3xIQR liegt, wird als einfacher oder milder Ausreißer, bei mehr als 3xIQR als extremer Ausreißer bezeichnet.
Je nach Definition werden alle Ausreißer als Kreise dargestellt, oder einfache Ausreißer als Kreise und extreme Ausreißer als Sterne. Je weiter die Werte von den Antennen entfernt sind, desto mehr müssen sie hinterfragt werden, ob ihnen nicht Messfehler o.ä. zugrunde liegen und sie aus der Auswertung ausgeschlossen werden.
Beispiel
Die bisher erläuterten Begriffe sollen nun anhand eines Beispiels veranschaulicht werden. Wir nehmen den folgenden Datensatz, der die in einem Test erreichten Punkte bei zehn Personen darstellt:

Die Daten werden im ersten Schritt nach der Größe sortiert und Median sowie Quartile berechnet. Die genauen Formeln für die Berechnung können in den Artikeln zu den Lage- und Streuungsparametern nachgelesen werden. In diesem Fall wurden die Werte von einem Statistikprogramm errechnet. Die Einheiten werden im Folgenden weggelassen:

Es ergeben sich folgende Werte:

Die Boxlänge bzw. der Interquartilsabstand IQR ergibt sich aus der Differenz der Quartile:
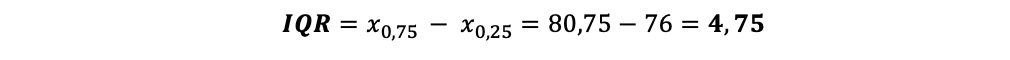
Die Antennen reichen vom jeweiligen Quartil aus bis zu maximal 1,5xIQR, also je:
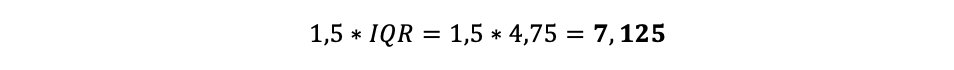
Einheiten nach oben und unten. Daraus ergeben sich für die Antennen:
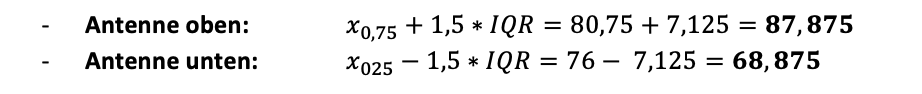
Da die Antennen nur bei im Datensatz enthaltenen Werten enden, die noch innerhalb dieses Bereiches liegen, ergibt sich:
- Antenne oben: 87,875 – der nächst kleinere Wert ist 82 und somit das obere Ende der Antenne – der Wert 88 ist als einfacher Ausreißer zu identifizieren, da er zwischen 1,5xIQR und 3xIQR liegt
- Antenne unten: 68,875 – der nächst größere ist Werte 73 und somit das untere Ende der Antenne
Mit den eben errechneten Werten ergibt sich folgender Boxplot:
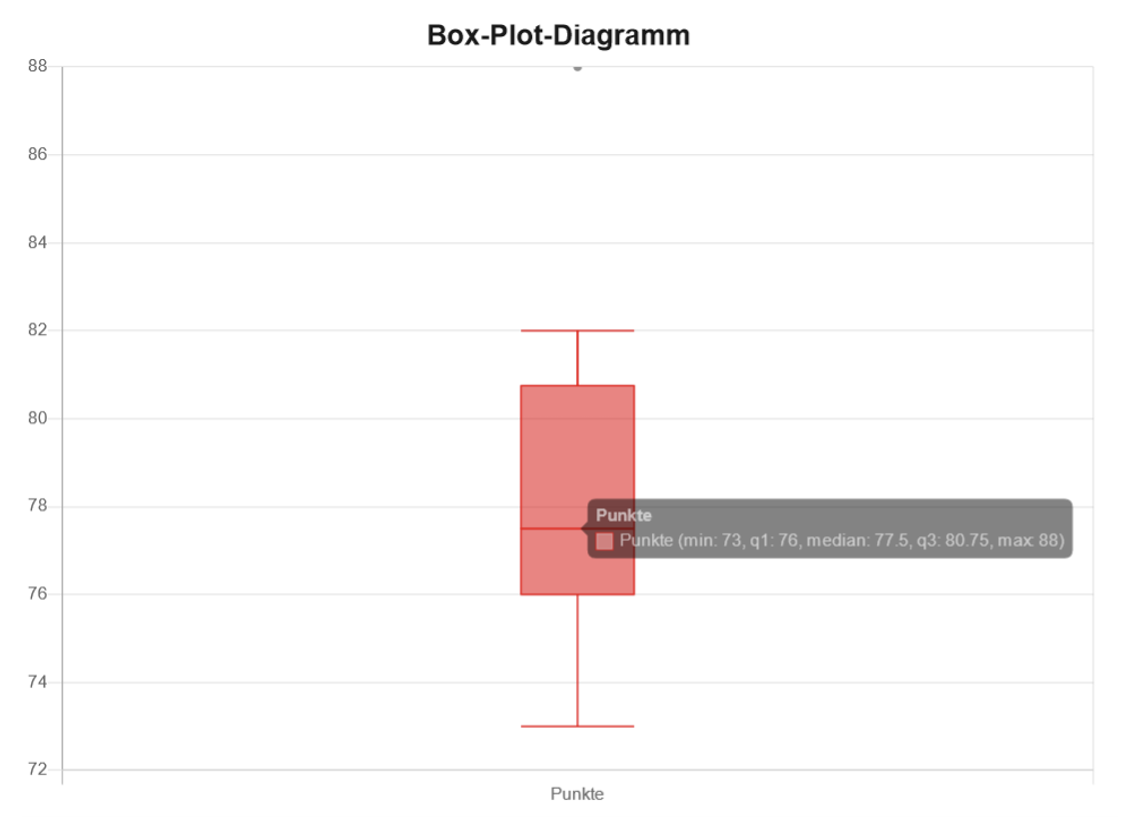
Zusammenfassung
Ein Boxplot zeigt alle wichtigen robusten Lage- und Streumaße sowie die Spannweite eines Datensatzes in einer Grafik. Stellt man mehrere Boxplots gegenüber, kann man Muster und Unterschiede zwischen den Stichproben erkennen. Boxplots geben jedoch keinen Aufschluss über die Art der Verteilung und über Häufigkeiten, dafür müsste man ein Histogramm verwenden. Bei bi- und multimodalen Verteilungen liefert der Boxplot keine sinnvollen Ergebnisse.
Gib deiner Arbeit den Feinschliff, den sie verdient.
Entfalte das volle Potenzial deiner schriftlichen Arbeiten mit Lektorat Plus und sichere dir den Weg zu einer herausragenden Note.
Jetzt Dokument hochladen