Binomialverteilung einfach erklärt
Inhaltsverzeichnis
- Einleitung
- Binomialverteilung und Bernoulli Variablen
- Herleitung der Formel
- Rechenbeispiel
- Voraussetzungen
- Zusammenfassung

Unsere Spezialisten unterstützen dich dabei, eine herausragende wissenschaftliche Arbeit abzuliefern.

Easy Thesis unterstützt dich beim Schreiben deiner Abschlussarbeit. Du wirst es lieben!
Einleitung
Die Binomialverteilung ist eine diskrete Verteilung, mit der Zufallsexperimente beschrieben und berechnet werden, die genau zwei verschiedene mögliche Ergebnisse haben. Mit Hilfe der Wahrscheinlichkeitsfunktion der Binomialverteilung kann man vorhersagen, wie wahrscheinlich es ist, unter n Versuchen ein bestimmtes Ereignis zu erzielen.
Der folgende Artikel erklärt, was eine Binomialverteilung ist, wie man sie berechnet und wofür man sie verwendet.
Bringe deine Noten auf das nächste Level!
Lass deine Arbeit von Lektorat Plus verbessern und sichere dir den Schlüssel zu akademischem Erfolg. 🎓
Mehr erfahren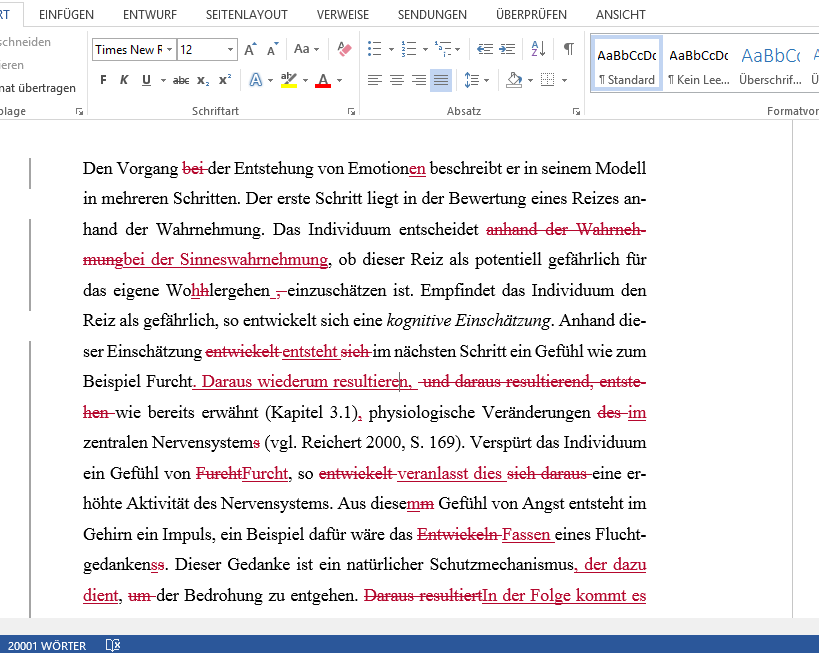
Binomialverteilung und Bernoulli Variablen
Die Binomialverteilung wird hergenommen, um ein bestimmtes mehrfach wiederholtes Zufallsexperiment mit genau zwei verschiedenen Ergebnissen zu beschreiben.
Somit ist die Binomialverteilung, im Gegensatz zur Normalverteilung beispielsweise, nicht für die Beschreibung aller Zufallsvariablen geeignet. Wie die Vorsilbe „bi“ bereits vermuten lässt, können binomialverteilte Variablen nur zwei verschiedene Werte annehmen wie „ja“/„nein“, „Kopf“/„Zahl“ oder auch „rot“/ „nicht rot“.
Viele Experimente lassen sich in ein Binomialexperiment umwandeln, indem man ein Ergebnis als „Erfolg“ und alle anderen Ergebnisse gegenteilig als „Misserfolg“ definiert. So könnte man beispielsweise beim Würfeln eine Sechs als „Erfolg“ und alle anderen Zahlen als „Misserfolg“ festlegen. Durch eine solche Umwandlung wird aus einem Zufallsexperiment mit sechs möglichen Ergebnissen ein Bernoulli-Experiment mit zwei möglichen Ergebnissen.
Variablen mit nur zwei möglichen Werten werden auch als Bernoulli-Variablen, das dazugehörige Experiment als Bernoulli-Experiment bezeichnet. Führt man dieses Experiment mehrmals hintereinander durch, spricht man von einer Bernoulli-Kette.
Den Begriff der Bernoulli-Verteilung gibt es hingegen nicht.
Von einer Binomialverteilung spricht man, wenn man ein Bernoulli-Experiment mit den Ausgängen x_1 und x_2 sowie den dazugehörigen Wahrscheinlichkeiten p und q mit einer bestimmten Anzahl von n wiederholten, voneinander unabhängigen Versuchen mehrfach durchführt.
Herleitung der Formel

Wir können also die Formel herleiten:

Binomialkoeffizient
Der Binomialkoeffizient (n k) (ausgesprochen n über k oder auch k aus n) gibt Auskunft darüber, wie viele Möglichkeiten es gibt, k Objekte in einer Gruppe aus n Wiederholungen anzuordnen oder wie viele Möglichkeiten es gibt, dass k Erfolge unter n Versuchen auftreten.
Er berechnet sich als:
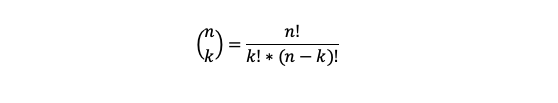
„Höchstens“ und „mindestens“ Ereignisse
Möchten wir statt „genau zweimal eine Sechs“ wissen, wie wahrscheinlich es ist, höchstens zweimal eine Sechs zu würfeln, müssen wir dafür drei Ereignisse aufsummieren und nach obiger Formel berechnen:
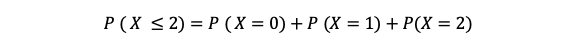
Verallgemeinert ergibt das die Formel:
m ist dabei die jeweilige Anzahl und k der Höchstwert, den wir erreichen wollen.
Während man kleine Werte noch per Hand aufsummieren kann, muss man größere Werte in einem Tabellenwerk nachschlagen oder sie von einer Software berechnen lassen.
Diese Formel kann jedoch nur die Maximalanzahl („höchstens k“) eines Ereignisses berechnen. Würden wir uns in dem vorherigen Beispiel mindestens zwei Sechsen wünschen, müssten wir die Wahrscheinlichkeiten für 2, 3, 4 und 5 Sechsen aufaddieren. Das ist bei kleinen n noch möglich, bei großen n hingegen nicht mehr. Hierfür arbeitet man dann mit der Gegenwahrscheinlichkeit: mindestens zwei Sechsen würde bedeuten: das Gegenteil von keiner oder einer Sechs:

Rechtsschiefe und linksschiefe Binomialverteilung
Ist die Wahrscheinlichkeit p für das Auftreten des Ereignisses x_1 gleich 0,5, ist die Binomialverteilung symmetrisch. Steigt die Wahrscheinlichkeit p auf mehr als 0,5, werden sich die Wahrscheinlichkeiten grafisch dargestellt nach rechts von der Mitte aus verschieben und die Binomialverteilung ist linksschief. Ist p kleiner als 0,5, verlagern sich die Werte grafisch nach links und die Verteilung ist rechtsschief.
Die folgende Darstellung zeigt mit den blauen Balken eine symmetrische Verteilung, mit den gelben eine linksschiefe und mit den orangen eine rechtsschiefe Verteilung.
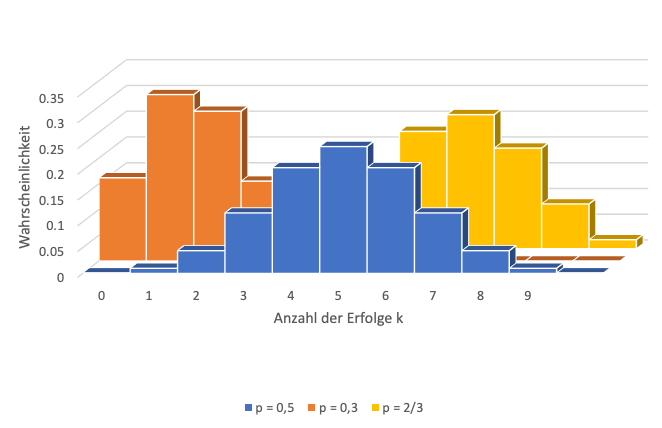
Wie bei allen anderen Wahrscheinlichkeitsverteilungen, ist auch bei der Binomialverteilung die Summe aller Wahrscheinlichkeiten für alle Ausgänge des Experiments gleich 1.
Ist die Stichprobengröße ausreichend groß (je nach Quelle bei n > 30 oder n >50), kann die Binomialverteilung mit Hilfe einer Normalverteilung angenähert werden. Auch die Schiefe der Verteilung wird mit zunehmendem n kleiner.
Lage und Streuparameter der Binomialverteilung
Auch für binomialverteile Zufallsexperimente lassen sich ein zu erwartender Mittelwert (siehe Artikel zu den Lageparametern) sowie die Streuung (siehe Artikel zu den Streuparametern) der Ereignisse um diesen herum ermitteln. Der Erwartungswert µ, die Varianz σ^2 und Standardabweichung σ lassen sich mit relativ einfachen Formeln berechnen.
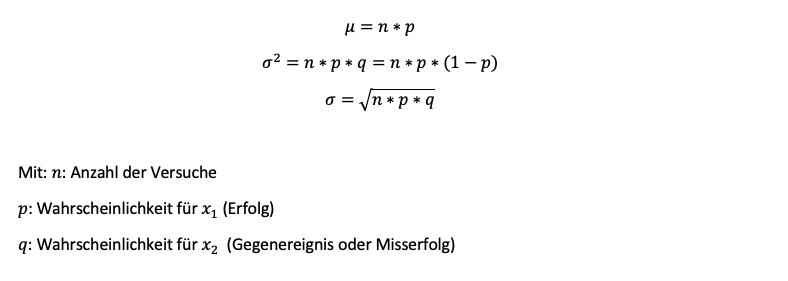
Rechenbeispiel
Nehmen wir als Beispiel zehn Runden des Spiels „Mensch ärgere Dich nicht“. Uns interessiert, wie hoch die Wahrscheinlichkeit ist, alle vier Spielsteine in diesen zehn Runden ist Spiel zu bekommen, also viermal eine Sechs zu Würfeln:
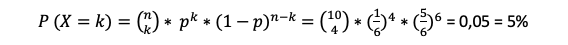
Die Wahrscheinlichkeit ist also ziemlich gering.
Berechnen wir alle Wahrscheinlichkeiten, wie häufig eine Sechs auftritt, erhalten wir folgende Verteilung:
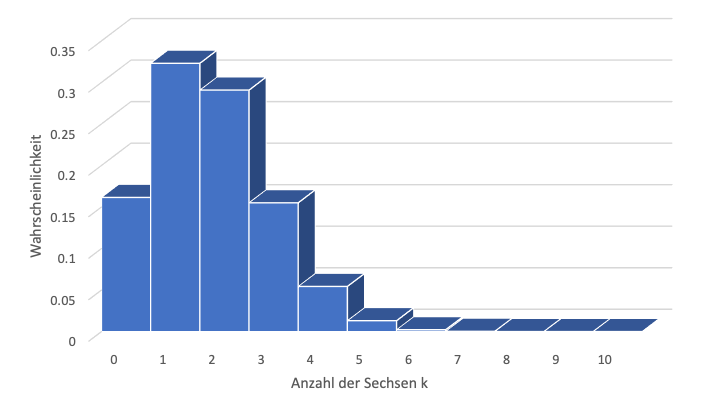
Mit der größten Wahrscheinlichkeit erwarten wir also einmal die Zahl sechs, mit der zweithöchsten Wahrscheinlichkeit zweimal die Zahl 6. Das wird auch anhand des Erwartungswertes deutlich. Dieser liegt für zehn Runden bei:
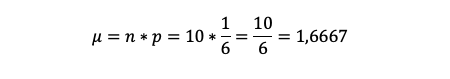
Bei zehn Runden würden wir also durchschnittlich 1,6667-mal eine Sechs würfeln.
Die Streuung liefert in diesem Fall kaum praktische Relevanz, aber wir berechnen zur Veranschaulichung trotzdem Varianz und Standardabweichung:
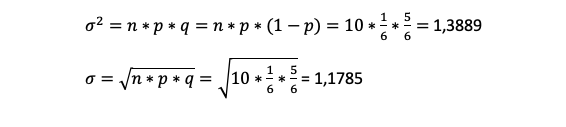
Voraussetzungen
Damit eine Binomialverteilung verlässliche Werte liefert, müssen einige Voraussetzungen erfüllt sein:
- Die Anzahl an Versuchen bzw. Wiederholungen n muss fest sein
- Die jeweiligen Versuche müssen voneinander unabhängig sein
- Jeder Versuch darf nur zwei verschiedene Ausgänge haben: x_1 und x_2
- Die Wahrscheinlichkeit p, muss über das gesamte Experiment hinweg konstant bleiben
Zusammenfassung
Einer Binomialverteilung, liegen mehrere aneinander gereihte Bernoulli-Experimente mit jeweils nur zwei verschiedenen Ausgängen zugrunde. Mit Hilfe der Wahrscheinlichkeitsfunktion kann man errechnen, mit welcher Wahrscheinlichkeit ein bestimmtes Ereignis auftritt. Diese Wahrscheinlichkeit errechnet sich aus der Anzahl der Möglichkeiten multipliziert mit deren einzelnen Eintrittswahrscheinlichkeiten. Über die Gegenwahrscheinlichkeit oder das Aufsummieren einzelner Wahrscheinlichkeiten können auch komplexere Ereignisse berechnet werden.
Ist die Wahrscheinlichkeit für einen Erfolg immer konstant und sind die Versuche voneinander unabhängig, liefert die Binomialverteilung tragfähige Ergebnisse. Ab einer großen Anzahl von Versuchen kann sie auch mit der Normalverteilung angenähert werden.
Gib deiner Arbeit den Feinschliff, den sie verdient.
Entfalte das volle Potenzial deiner schriftlichen Arbeiten mit Lektorat Plus und sichere dir den Weg zu einer herausragenden Note.
Jetzt Dokument hochladen